Zur Frage der verschiedenen wohltemperierten Stimmungen

Meine Berechnungsgrundlagen

Um eine Aussage über die zu erwarteten Klänge zu bekommen, habe ich die Differenzen und Schwebungen berechnet, die bei den verschiedenen Intervallen entstehen können, zehn von jedem Grundton aus (nur zehn, weil deas elfte Intervall, der "Tritonus", die halbe Oktave zwischen Quarte und Quinte, immer "schlecht" klingt).

Dafür ist zuerst einmal eine definierte Intervallgröße nötig. Bei Quint und Quart ist das klar, 2:3 und 3:4.

Bei den Terzen setzt es sich logisch fort: 4:5 und 5:6. Auch über die Sexten gibt es keine Diskussionen, nur lässt sich die Zahlenfolge nicht fortsetzen (5:6 → 4:5 → 3:4 → 2:3; nun müsste 1:2 kommen, das ist aber schon die Oktave). Darum sind die Verhältniszahlen jetzt etwas komplizierter, 3:5 und 5:8.

Soweit besteht Einigkeit.

Werden die Intervalle kleiner, müssten logischerweise die Verhältnisse so fortgesetzt werden, 6:7 und 7:8 für die große und kleine Sekunde. Das ist aber nicht so, das Schwingungsverhältnis 6:7 liegt zwischen kleiner Terz und Ganzton.

Der Ganzton, die große Sekunde, hat das Schwingungsverhältnis 8:9 oder 9:10, je nachdem, ob man von den Quinten her stimmt (pythagoräisch 8:9) oder von den Terzen (mitteltönig 9:10). Es gibt dafür die Bezeichnungen großer Ganzton und kleiner Ganzton. Bei der gleichstufigen Stimmung wird das Intervall gar nicht beachtet, sondern ergibt sich als Differenz zwischen Quinte und Quarte. (Näheres bei wikipedia unter „Ganzton“.)

Für die Berechnung hab ich 8:9 genommen, aber unter die Spalte die tatsächliche Größe des Ganztons angegeben. 9:8 ist als Kommazahl 1,125; 10:9 ist 1,1111… So lässt sich erkennen, ob es sich bei der Stimmung um kleine oder große Ganztöne oder gar nichts von beidem handelt. Für die bessere Übersichtlichkeit musste diese Angabe allerdings später wieder gelöscht werden ;-)

Bei der kleinen Sekunde wird es noch schwieriger: pythagoräisch ergibt sich ein Verhältnis von 256:243. Es wird sogar das Verhältnis 2048:2187 angegeben. Auch 24:25 und 128:135 werden genannt. Da erscheint mir der „diatonische Halbton“ mit 15:16 vernünftig. Er wird in keiner Stimmung erreicht, dient aber als Maß, weil dazu Schwebungen hörbar sein können (mit 16-facher Frequenz des Fehlers)

Noch schwieriger wird es bei den Septimen:
4:7 und 8:15 werden für die Septime angegeben. Diese Verhältnisse werden aber nie erhalten. Dagegen wird in 8 der 12 Intervalle bei der Stimmung mit 10 reinen Quinten das Verhältnis 9:16 für die kleine Septime genau erhalten und in 6 von 12 Intervallen bei der Stimmung mit 9 reinen Quinten (der HaDEs-Stimmung). Es hat also Sinn, dieses Verhältnis 9:16 als Maß zu nehmen, denn das hört man jedenfalls bei einem Teil der Intervalle tatsächlich.

Bei der großen Septime gibt es nur einen Kompromiss:
Das Verhältnis 9:17 stimmt sowohl bei der gleichstufigen Stimmung ziemlich genau (es ist 0,06% enger) als auch bei der neuen Stimmungen mit Abweichungen nach beiden Seiten (enger und weiter).
Was man tatsächlich als Schwebungen hört, richtet sich ja nach der Differenz der Frequenzen (zwischen dem idealen und dem tatsächlichen Ton) und dem jeweiligen Intervall, wie es unter „harmonische Grundlagen“ schon erklärt wurde.

So ergibt sich für die verschiedenen Intervalle folgende Rechnung:
Quinte: Schwebung = das doppelte der Differenz (Differenz x 2)
Quarte: Schwebung = Differenz x 3
große Terz: Schwebung = Differenz x 4
kleine Terz: Schwebung = Differenz x 5
große Sekund: Schwebung = Differenz x 8 (nur theoretisch, nicht zu hören)
kleine Sekund: Schwebung = Differenz x 15 (nur theoretisch, nicht zu hören)
kleine Sext: Schwebung = Differenz x 5
große Sext: Schwebung = Differenz x 3
kleine Sept: Schwebung = Differenz x 9 (nur theoretisch, nicht zu hören)
große Sept: Schwebung = Differenz x 9 (nur theoretisch, nicht zu hören)

Zur Berechnung der Schwebungen und der relativen Abweichungen der Intervalle habe ich ein Programm in Excel geschrieben:

Aus dem Grundton werden die anderen Töne der Tonleiter nach der jeweiligen Temperatur-Vorschrift berechnet (wieviele reine und unreine Quinten enthalten sind); aus den verschiedenen Frequenzverhältnissen bei den verschiedenen Intervallen wird das reine Intervall berechnet und aus der Differenz mit der berechneten Tonleiter wird sowohl die relative Abweichung als auch die Anzahl der Schwebungen berechnet.

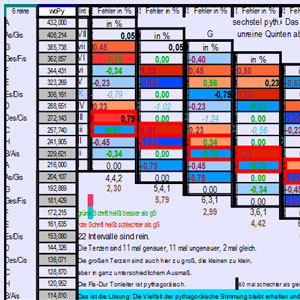
Es ergibt sich daraus eine treppenartige Tabelle, die alle 120 Intervalle mit relativem Fehler und Schwebungszahl im mittleren Hör-Bereich anzeigt (Mitte des Klaviers).

Weil das ziemlich unübersichtlich ist, habe ich daraus die Intervalle heraus gezogen, die für die normalen Dur- und Moll-Akkorde gebraucht werden. Daraus entstand eine zweite Tabelle, in der für jeden Akkord die Schwebungen der auftretenden Intervalle angezeigt werden: kleine und große Terz, Quint, Quart und kleine oder große Sext (für Dur oder Moll). Weil das immer noch viele Zahlen sind, habe ich sie in Grautönen unterlegt, je dunkler, umso stärker ist die Abweichung von den reinen Intervallen. Die Abweichungen wurden anschließend von % in Cent umgerechnet nach der Formel
H_[Cent] = 3986,313714 · lg (U_[%]/100 + 1)

So lässt sich einigermaßen gut abschätzen, wie eine Stimmung klingen wird.